研究メモ。
タイトルについて日本語でざっくり書いてある記事がなかったので書いておきます。
Amberで温度圧力一定(NPT)のMDをする場合、圧力制御法は2つあって(Amber18現在)、Berendsen法とMonte Carlo(MC)法。
これらはMDのインプットでbarostat=1(Berenden、デフォルト)、またはbarostat=2(MC)と指定できるわけですが、これらはどう違うのか?
簡単に言うと、
Berendsenは古くから使われている方法なんだけど、厳密にはNPTアンサンブルをサンプリングできないという問題がある。
一方でMCは、最近(たしかAmber14以降)導入された方法で、厳密にNPTアンサンブルを生成し、しかも周期境界条件を使う場合は計算が速い、というメリットがある。
というわけで基本的にはMCを使う方が良いことになります。
以下でもう少し詳しくそれぞれの手法を見ていきます。
1. Berendsenの方法
圧力と体積は反比例するというのを高校の化学で習ったと思います。
PV=一定
(Pが圧力で、Vが体積)
だから圧力は、体積を大きくしたり小さくしたりして制御できます。
なので、どのように体積を変えるかがBerendsen法とMC法の違いになります。
Berendsenの方法は、ある時間tの圧力P(t)が緩和時間τ(タウ)後に設定した圧力P0になるように体積(シミュレーションボックスの大きさ)を変えます。
式で表すと、

この式はP(t)とP0の差が、緩和時間τの間に減っていって0になるよう調整することを示しています。
τのデフォルトの値は1 psです。もしMD結果で圧力が不安定に見えるなら、もっと長い値(5 psくらい)にしてみると良いです。
ちなみにボックスサイズだけを変えてしまうと、例えば小さくすると分子が箱の外に出てしまったり、逆に大きくすると真空ができたりしてしまうので、箱の中の分子の位置(座標)も一緒に変えてます。
Berendsenの圧力制御法については、ざっくり言うとこんな感じです。
もっと詳しくは、奥村久士先生が良い日本語の解説記事を書いてくださっていますのでこちらをご参照ください。
『分子動力学シミュレーションにおける温度・圧力制御 第 5 回:パリネロ・ラーマンの方法,圧力一定のガウス束縛法, 圧力一定のベレンゼンの方法』
http://okweb.ims.ac.jp/molsim5-3.pdf
2. Monte Carlo法
この方法はなんと圧力を計算しません。
MD計算において圧力を計算するにはビリアル定理を使います。
詳細は割愛しますが、特に周期境界条件を使う場合は遠くの分子との相互作用も考えないといけないので、かなりの計算コストがかかります。
なので圧力を計算するBerendsenの方法に比べて、圧力を計算しないMC法は(特に周期境界条件を使う場合に)計算が速い、というメリットがあります。
ではどのように圧力を制御するかというと、
①とりあえずランダムに体積を決める。
②その体積に実際に変更するかどうかをメトロポリス法で判定する。
という手順です。
なのでメトロポリス法の判定結果によって、体積が変わったり変わらなかったりします。
メトロポリス法っていうのは、ランダムに生成された状態の中から特定の状態を選ぶ基準のことで(Metropolis criterion)、この基準で選ばれた状態の集団(アンサンブル)は平衡状態のアンサンブルと厳密に一致することが知られています。
一応この判定法における採択確率の式を紹介します。

(Amber16 manual, p. 514より)
http://ambermd.org/doc12/Amber16.pdf
つまり、新しくランダムに決められた体積に対して一番右の項を計算して、結果がもし1より小さ大きければ、その状態は確率1(100%)で採択。
そうでなければ、その結果の値の確率で採択する、という意味です。
より詳しくは上のAmberマニュアルをご参照ください。
最後に同じシミュレーション系で二つの圧力制御法を使ってみて、体積(シミュレーションボックスのサイズ)がどのように変化したのかプロットした図がこちらです。
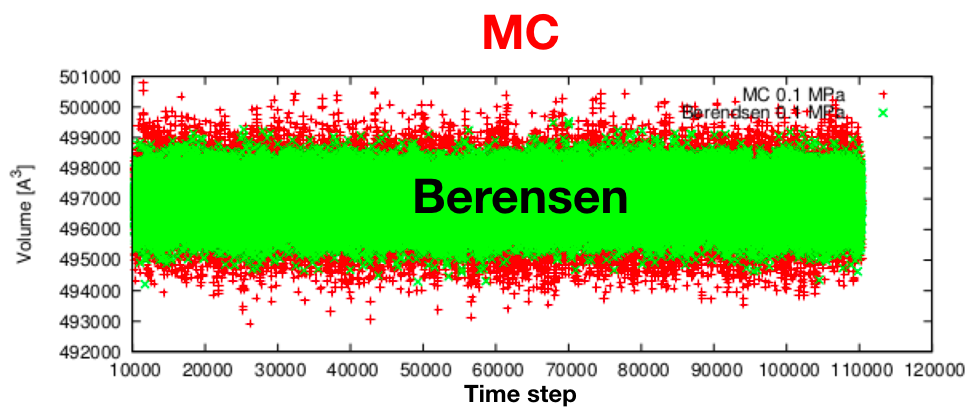
この場合、MCの方がBerendsenよりも体積の揺らぎが大きいですね。
体積が違う状態をランダムに生成するのでいろんな体積になりやすいのかもしれません。